Mathematicians solve the infamous “moving sofa problems”

Mathematicians solve the infamous “moving sofa problems”

Jack Matag Jeanna Bryner is edited

Mathematicians wrestled on a narrow horn and lamented, “Is this uniform?” Geometry’s “Transfer sofa problem” is the largest shape that allows you to turn a right angle in a narrow corridor without getting stuck. The problem remained unresolved for almost 60 years until November, when Jeanon Baek, a postdoc, postdoc at Yonseyi University, posted a papers claimed to solve it. BAEK’s evidence has not yet been thoroughly peared, but the first pass from mathematicians who know the problem of Baek and Moving Sofa seems optimistic. You can see why BAEK 119 took a comedy rosgerer friend I said in one word.

This solution rarely helps you on a moving day, but as the frontier mathematics is more abstract, mathematicians specially use unresolved problems that can be understood. In fact, the popular mathematical forum Mathoverflow maintains a list of “a particularly famous and open problem that everyone can understand”, and the problem of moving sofas is currently ranked second in the list. Masu. Nevertheless, all evidence will expand our understanding and use the techniques used to solve the problem of the moving sofa will lend yourself to other geometric puzzles in the future.

The rule of the problem that Canadian mathematician Leo Moser first poses in 1966 is accompanied by a hard shape that rotates a right angle in the corridor. The sofa can be an arbitrary geometric shape. You don’t have to look like a real sofa. Both shape and corridor are two -dimensional. Imagine that the sofa is too much to lift. Just slide.

About the support of science journalism

If you are enjoying this article, consider supporting journalism that has won. Subscription. By purchasing a subscription, it will help you secure the future of a story that has an impactful story that forms our world today.

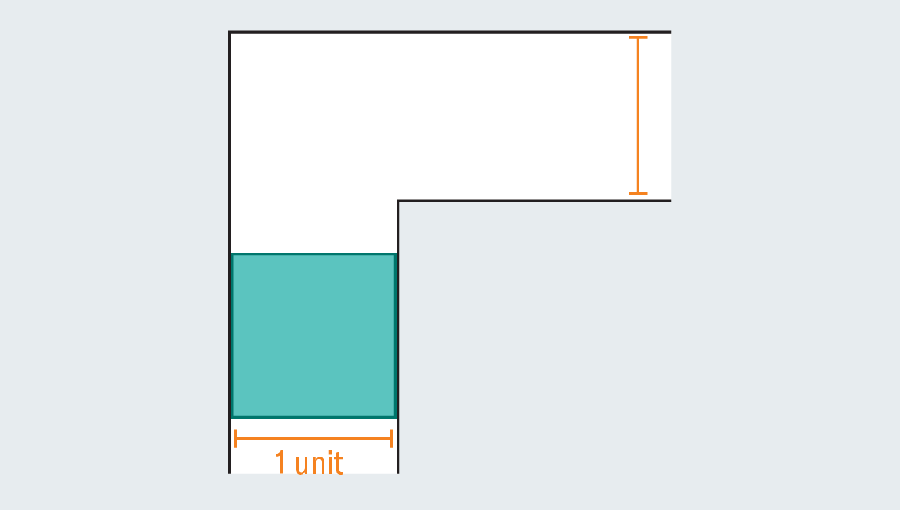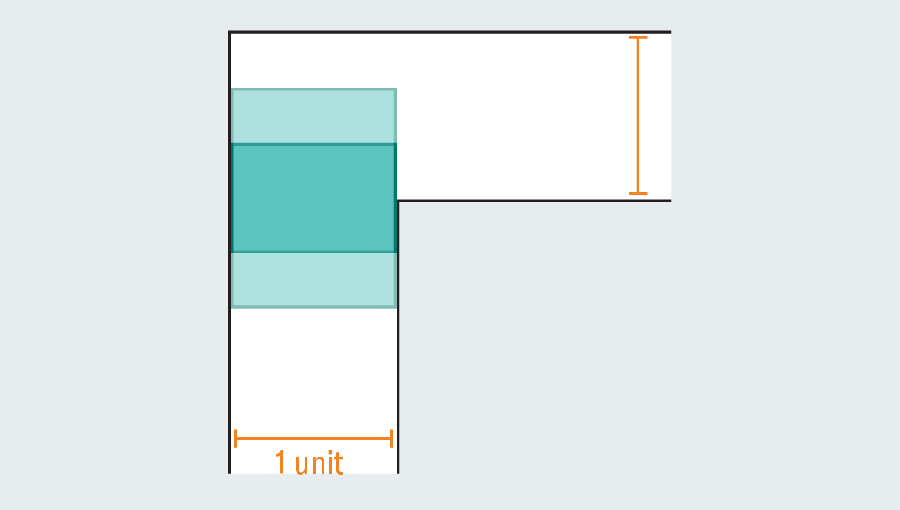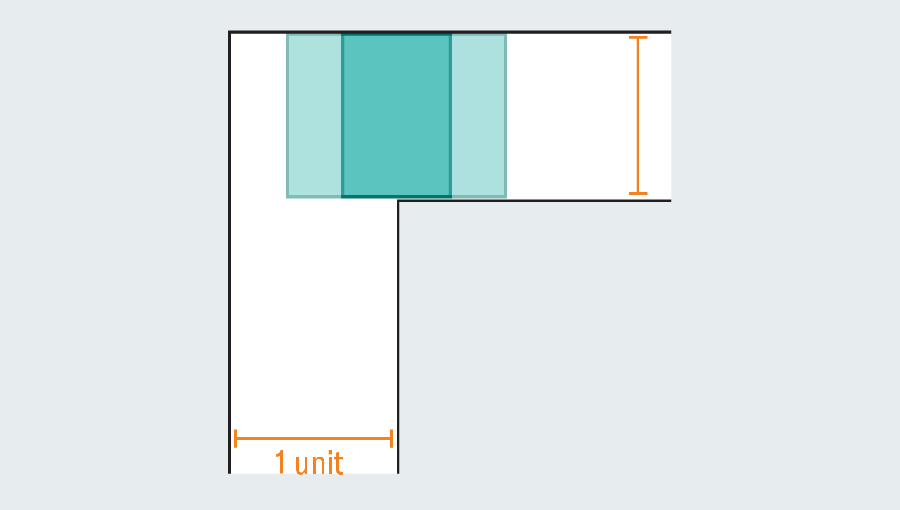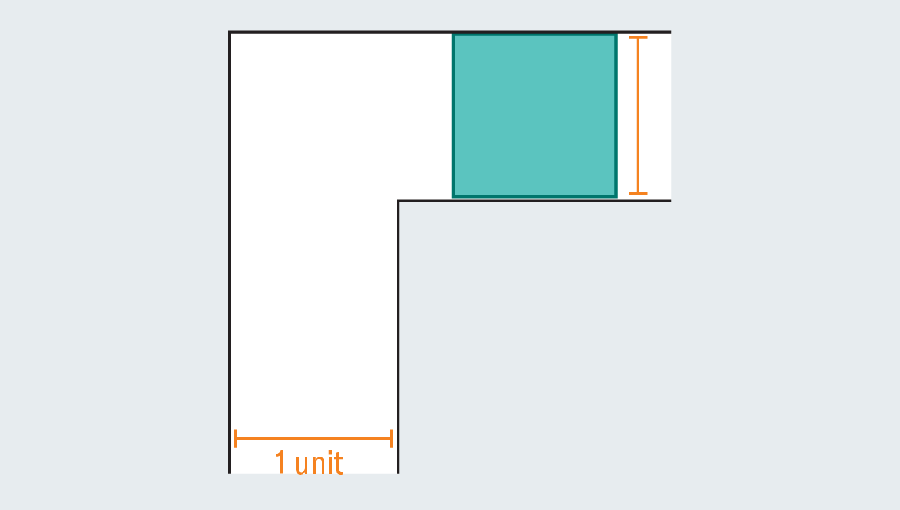
A simple tour of the history of the problem revealed a wide range of efforts that mathematicians poured. They were not couch potatoes. What is the biggest shape that you can narrow down in the sky corridor? If each leg in the corridor measures one unit (a specific unit is not relevant), you can easily scute one square of one passage. Forming a rectangle to extend the square immediately fails. This is because there is no room to turn when hitting the kink in the corridor.

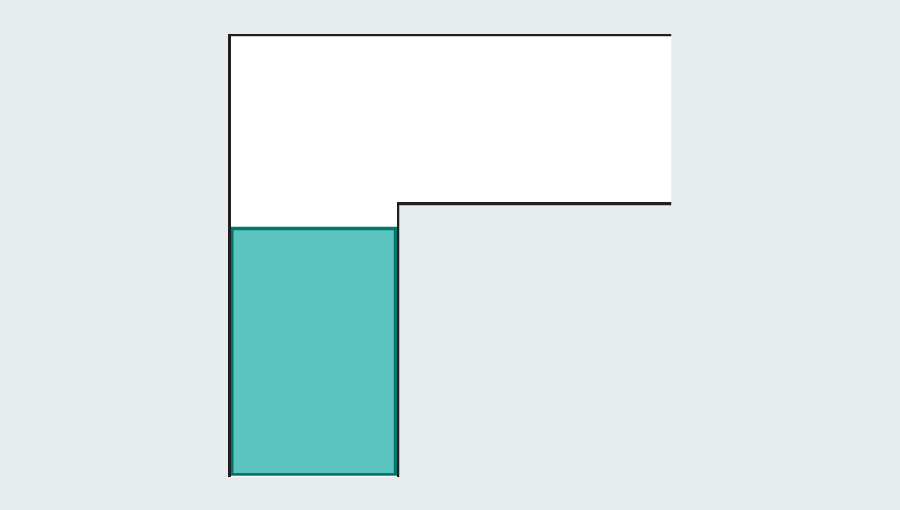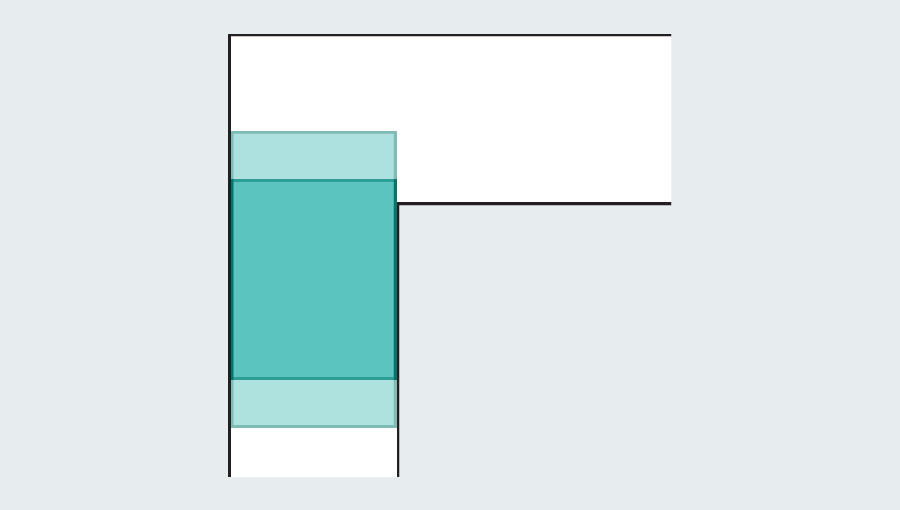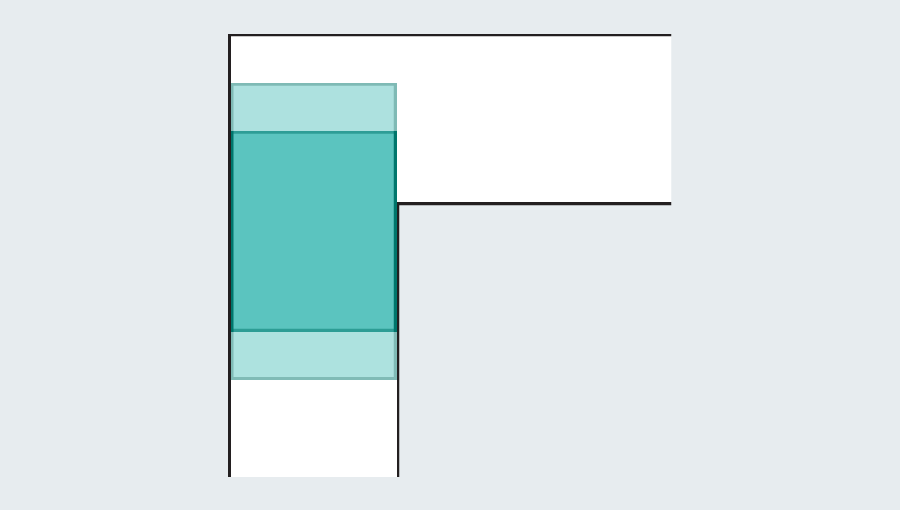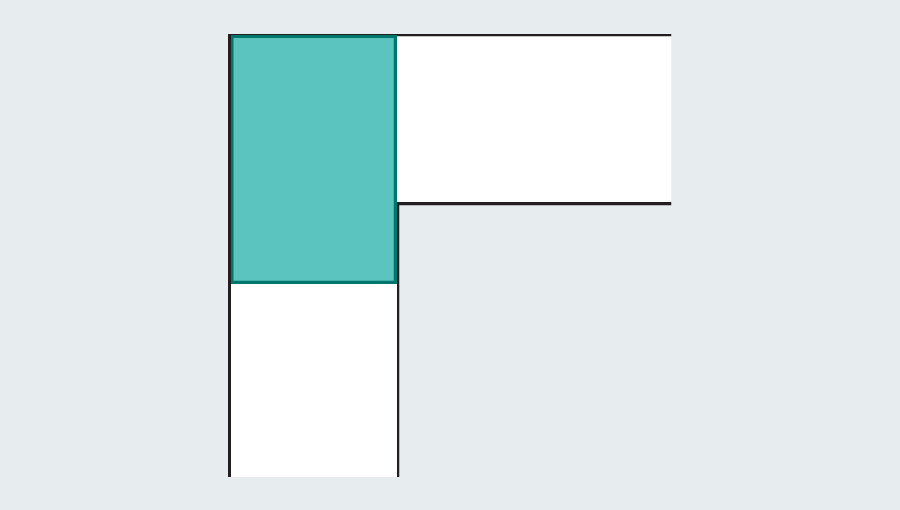
However, mathematicians noticed that the introduction of a curved shape could grow. Let’s consider the semicircle of 2 diameter (straight base). When you hit the turn, many of them still protrude with the first foot of the corridor, but round edges leave enough rooms to clean the corners.

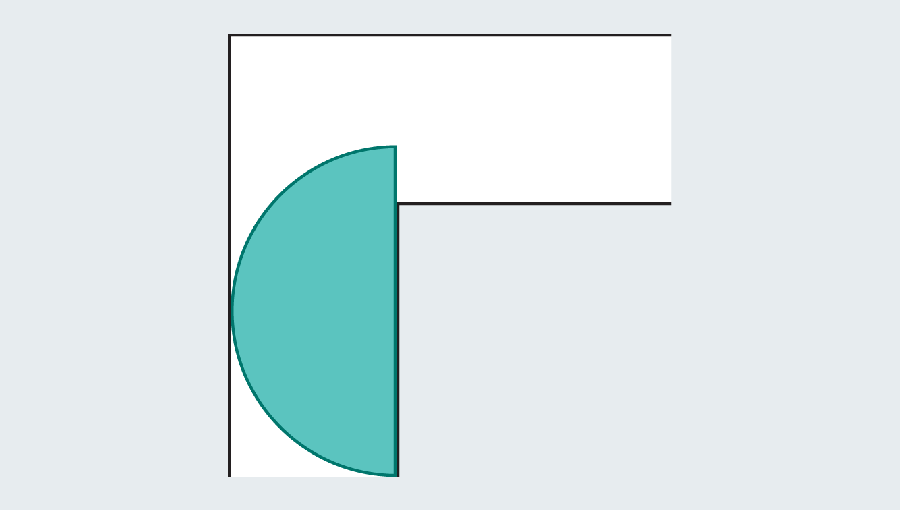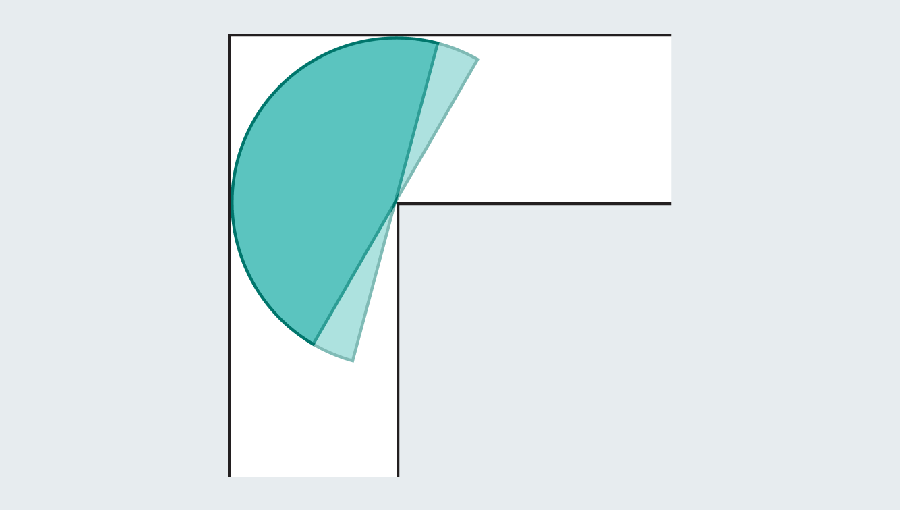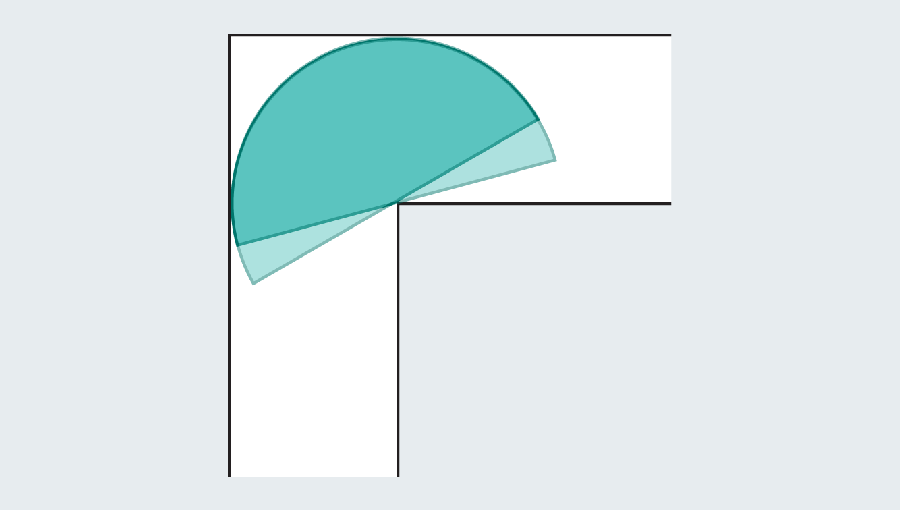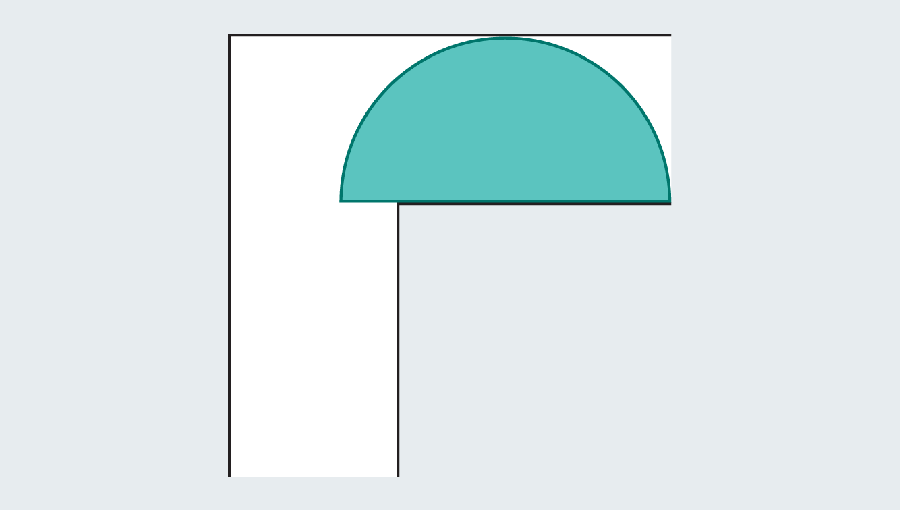
The goal is to find the largest sofa that turns the horns and slides. If you come to the high school geometric ceremony, you can calculate the semicircular area as π/2 or about 1.571. The semicircle is significantly improved than the square, which had only one area. Unfortunately, both look strange in the living room.

To solve the problem of moving sofa, not only optimize the size of the shape, but also path The shape is crossed. The setup allows two types of movements, slide and rotation. The square sofa slipped, but the semicircle slipped, rotated around the corner, and then slipped on the other side. However, the object can be slid and rotated at the same time. Dan Romik, a mathematician at California University Davis, pointed out that solutions in question should optimize both types at the same time.

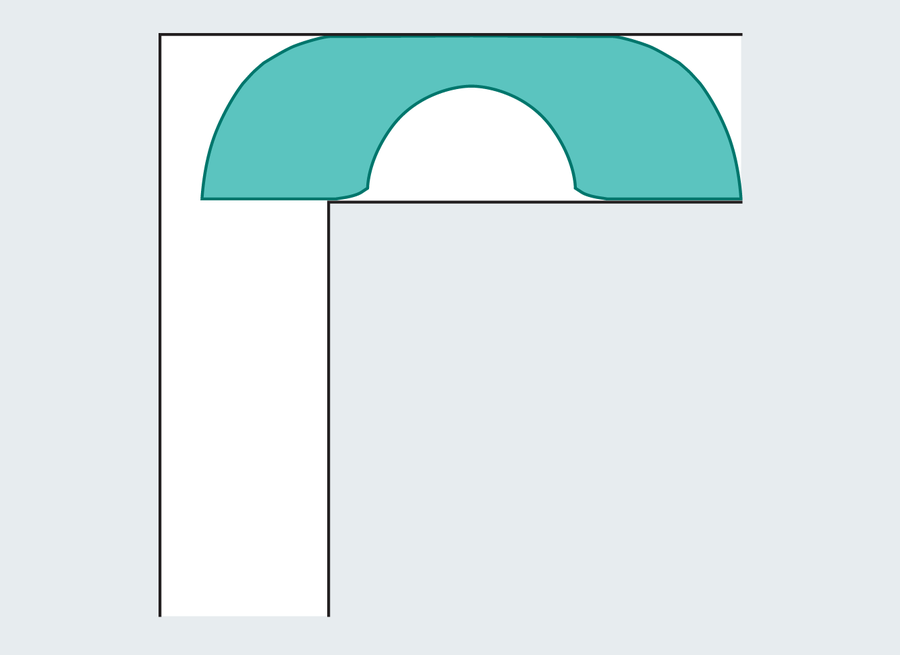
British mathematician John Hamerslie discovered to grow in the semicircle in 1968. can If you are engraving a lump to deal with the troublesome corner, buy a big sofa for you. In addition, the Hammersley sofa uses hybrid slides and rotation movements. The result sofa looks like a landline phone:

If you optimize different variables, you will get a sofa of π/2 + 2/π, that is, about 2.2074. This is a large upgrade from a semicircle, similar to a love seat to a sexual movement. However, progress has been stuck there for 24 years. The next major improvement is the last. In 1992, Joseph Garber published a masterpiece of mathematical carpentry work.

You will be allowed to feel the digital now. The gerver sofa looks the same as the Hammersley sofa, but has a much more complicated structure. Gerber connected 18 different curves to form his shape. Detailed tests can find some differences, especially the interesting edges at the base of the rounded cutout.

The area of ​​Gerver’s victory is measured by 2.2195 units. Surprisingly, Hammersley’s relatively simple sofa fell only about .012, although it was optimal. The squeals were only larger than their predecessors, but Gerver suspected that he had reached his maximum size as much as possible. He couldn’t prove it. And I couldn’t do anyone for another 32 years.

BAEK has obtained a doctorate. In 2024, he wrote his paper on the problem of moving sofas and contributed to some progressive insights. In the same year, he sewed all his fresh ideas and sewn to an impressive Opus to prove that there was no sofa larger than Garber could squeeze the corridor. Solving a long -standing problem is a dream for mathematicians, and it goes without saying early career. If BAEK’s work endures the scrutiny, he will probably notice that the demand for professors is high. Unless he pivot for furniture production.