Explaining the history of Venn diagrams and their popularity outside of mathematics

in his book mathematical universe, Mathematician William Dunham wrote of John Venn’s eponymous legacy, the Venn diagram, that “no one in the long history of mathematics has accomplished a greater feat.” Venn diagrams may not have solved long-standing unresolved problems, but certainly these interlocking rings deserve more recognition. Their compact representation of group relationships explains their enduring appeal in classrooms, infographics, and internet memes.

More than just a visual aid, Venn diagrams help solve everyday logic problems and pose surprising geometric problems. Have you ever seen a proper Venn diagram with four overlapping circles? No, you can’t. Ben himself discovered this and came up with a clever fix, but this only created a deeper geometric puzzle that mathematicians still study today.

Benn published diagrams in 1880 as a way to visualize the advances in modern logic. Later, they found applications in a closely related branch of mathematics called set theory, which focuses on collections of objects. A Venn diagram usually consists of overlapping circles, each representing some set of elements (for example, something cute or a Broadway show). The overlap region between two circles contains elements that belong to both sets (e.g. “cat”). It’s much like using scatter plots in statistics or drawing shapes in geometry. look Our own problems often reveal it.

About supporting science journalism

If you enjoyed this article, please consider supporting our award-winning journalism. Currently subscribing. By subscribing, you help ensure future generations of influential stories about the discoveries and ideas that shape the world today.

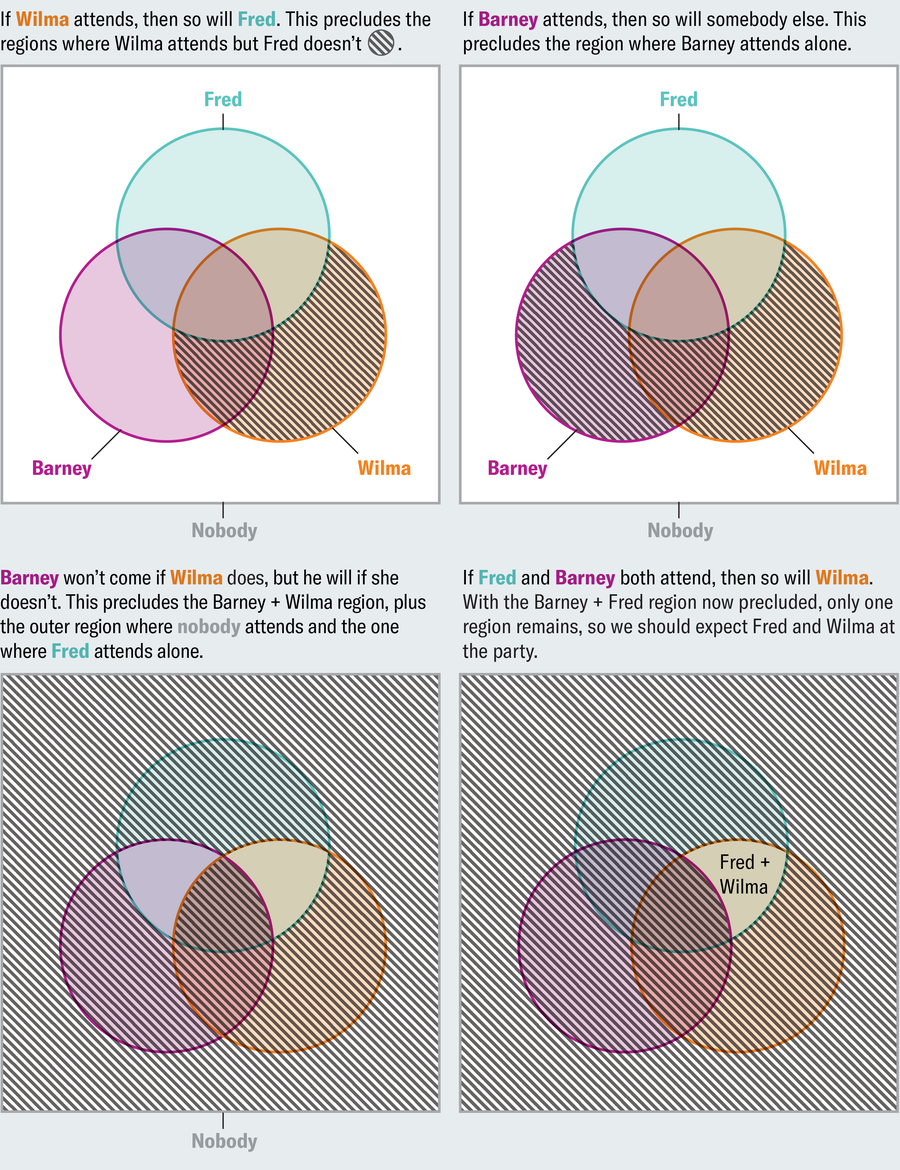
Imagine you’re planning a dinner party and dealing with your friends’ whimsical tastes. If Wilma attends, Fred will too. If Bernie is going to be there, someone else will be too. If Wilma comes, Barney won’t come, but if Wilma doesn’t come, Barney will come. If both Fred and Barney are present, Wilma will also be present. Who do you expect to appear? This pose is difficult to perform when only the text is given. Venn diagrams provide a systematic way to visualize and solve it. Each statement rules out some possible outcome. Indicate this by shading the corresponding area in the Venn diagram.

Most Venn diagrams you come across depict two or three overlapping circles, but what if there are four or more sets to consider?

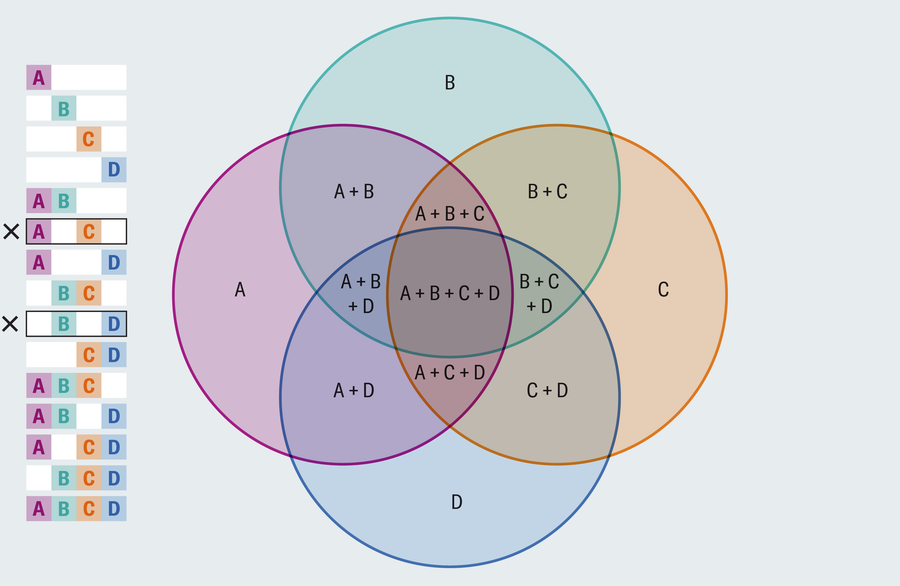
Did you find the problem? There is no region where only A and C overlap and do not contain another region. The same goes for B and D. A good Venn diagram shows all combinations of intersections. Rearranging the layout doesn’t help. All four circle drawings have the same flaw.

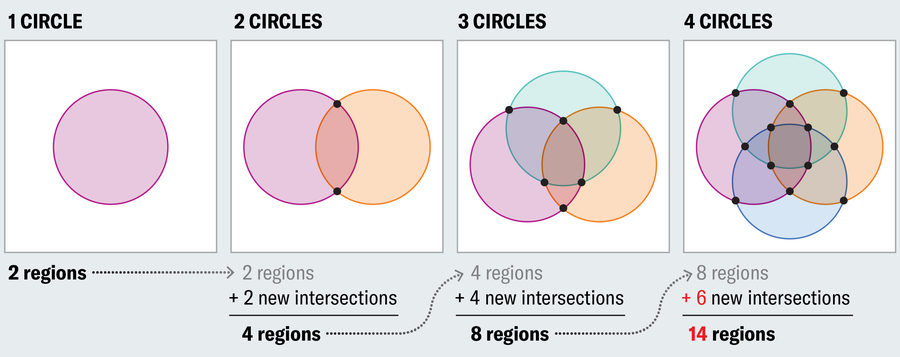
To understand why, start with a single circle and notice that it establishes two areas: interior and exterior. Adding a second set of elements (new circles) doubles the likelihood, so the number of regions must also double (first set, second set, both sets, neither set). (also not used). The only way to do this is to intersect the second circle with the first at two points (if they touch at only one point, there will be only three areas: the first set, the second set, or neither). This trend continues, and if we want to represent all logical possibilities, we need to double the number of areas for each new circle. However, the number of new regions cannot exceed the number of new regions. intersectionnew circles can only intersect existing circles at two points each. This works fine if you want to add a third circle because you need to add four regions and the new circle intersects the two existing circles at two points each, for a total of four new intersection points. But in the fourth circle it breaks down. There you need 8 new areas, but only 6 new intersections can be collected.

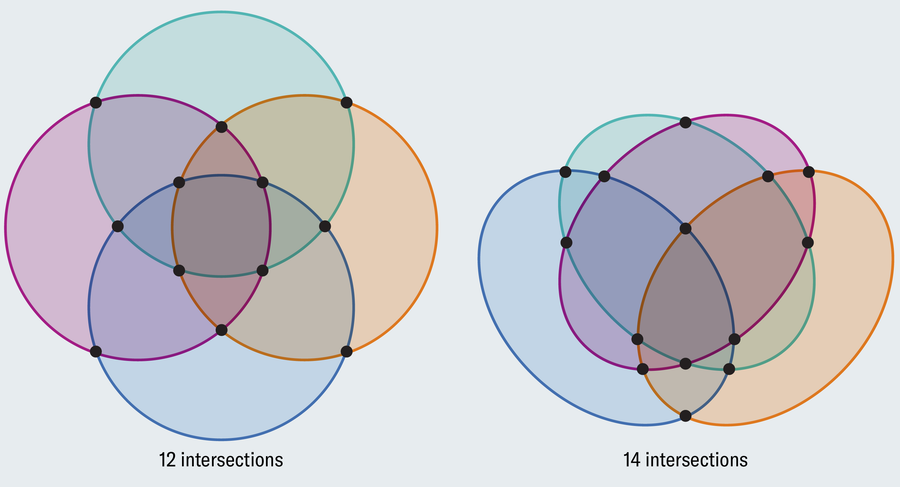
Of course, you don’t have to limit yourself to circles. You can easily trace a squiggly loop through the three-circle diagram to cut out the required number of areas, but the elegance of the diagram will be lost. four intersections sphere Although a reasonable number of regions can be represented, three-dimensional visuals are difficult to parse. John Benn knew the shortcomings of the circle, so he proposed an ellipse to represent the four sets.

Unlike circles, two ellipses can intersect at: 4 point. This overcomes the circle limitation, but only temporarily. The ellipse works for 4 and 5 sets until it fails, just like the circle. As the number of sets increases, more exotic shapes are needed to depict them.

It can be reasonably argued that Venn diagrams lose their usefulness when the set of elements exceeds four. The image of four ellipses is already quite chaotic. Perhaps for more than 5 sets, visual presentation should be abandoned. But practicality is not what energizes mathematicians, it is not as important as beauty or curiosity. Venn diagrams were initially applied to logic and set theory, but the four-circle conundrum raised interesting problems in geometry. That seed blossomed into an interesting study of the geometry of Venn diagrams that continues to this day.

Benn and his successors believed that an ellipse could not represent all 32 areas needed for five sets of diagrams. It wasn’t until 1975 that mathematician Branko Grünbaum proved them wrong with an example.

Note also that Grünbaum’s diagram shows a pleasing rotational symmetry. After one-fifth of a full rotation, it returns to its original position and its original shape remains unchanged. Typical 2-circle and 3-circle Venn diagrams share this property. A two-circle Venn diagram rotated 180 degrees (or a three-circle Venn diagram 120 degrees) looks the same. However, the four ellipsoids have no rotational symmetry. Can it be fixed? What do 2, 3, and 5 have in common that 4 doesn’t?

In 1960, David W. Henderson, then an undergraduate at Swarthmore College, answered this question with a surprising discovery (Stan Wagon and Peter Webb later filled in some of the gaps): The rotationally symmetric Venn diagram This is possible only if the numbers in the set are prime numbers – numbers that are divisible only by 1 and themselves, such as 2, 3, and 5, but not by 4. Henderson merely showed that the set must have a prime number, and is not always divisible. Design a symmetric Venn diagram for all prime numbers. So began a contest to find a bigger example. Here’s a wild-looking 11-set Venn diagram by Peter Hamburger.

Mathematicians at the University of South Carolina solved this problem in 2004 by showing that a rotationally symmetric Venn diagram exists for each set of prime numbers. If you think this is what caused mathematicians to put away their pencils and stop studying Venn diagrams, you’re not keeping up. Instead, the community is looking for individuals with heightened aesthetic standards and more sophisticated characteristics.

In our opening quote, we argued that Venn diagrams are overvalued. Even those who agree have to admit that there is a strange fascination with them. Take a series of interesting topics in logic, geometry, and visualization, and you’ll find a Venn diagram at the intersection.