Create a dating reality show that’s unique in the ways that matter. First, we will rent a villa on a southern island. Then we bring in five men and five women, each with their own (heterosexual) dating preferences. However, our goal is to love island Franchise: We want absolutely zero drama. Can everyone pair up with a partner and stick with them without jealousy rearing its ugly head?
Mathematicians call this dilemma the “stable matching problem” or the “stable marriage problem.” And while matters of the mind may be fickle, researchers have shown that by using simple algorithms, you can: everytime Find a stable match set between all members of two equal-sized groups. The late mathematician Lloyd Shapley shared the 2012 Nobel Prize in Economics for the discovery of this algorithm. There’s a good reason for that. The algorithm is still used today to connect residents with hospitals, children with schools, and even influences dating apps. algorithm.
According to mathematicians, a relationship is stable when neither person has a better option, at least when there is no one who is also interested in them. So the instability is: Imagine that Alice is currently paired with Bob and Charlie is currently paired with Darlene. However, Bob is secretly in love with Darlene, and Darlene can’t bear the thought of spending another day with Charlie. Mathematicians call this situation unstable because Bob and Darlene appear ready to leave their partners behind and run away together.
About supporting science journalism
If you enjoyed this article, please consider supporting our award-winning journalism. Currently subscribing. By subscribing, you help ensure future generations of influential stories about the discoveries and ideas that shape the world today.
The same dilemma occurs outside of love. Shapley and mathematician David Gale first described this problem as a college admissions problem. What kind of application process ensures that colleges and applicants, each with their own unique preferences, are satisfied with their choices? In 1962, Gale and Shapley (in the dating show example, men and women), but we showed that there is always a set of combinations for which all matches are stable. Additionally, they provided a simple process, or algorithm, to take everyone’s rankings and construct relatively satisfactory pairs.
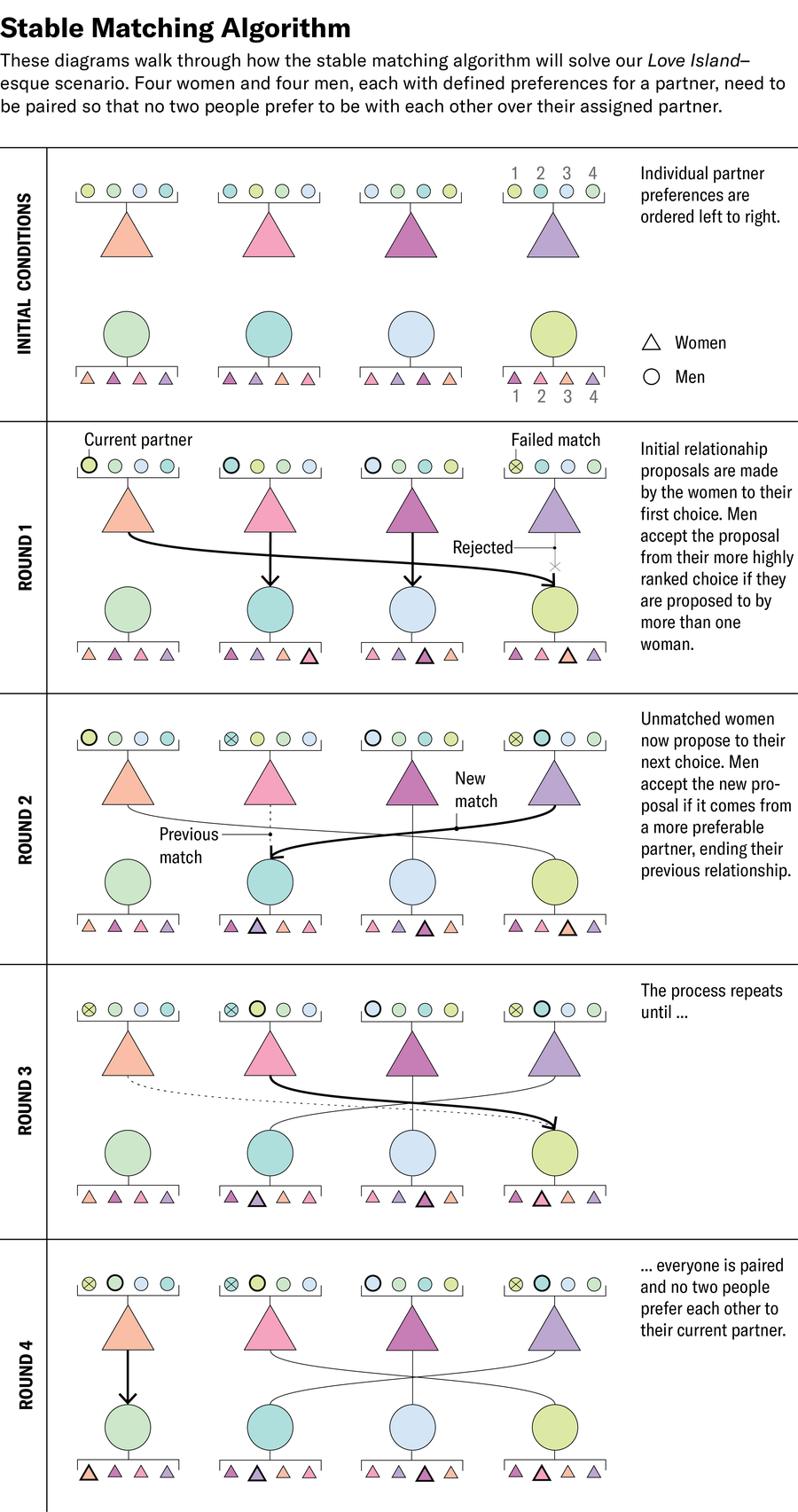
Here’s how it works: To find stable, drama-free partnerships among the 10 dating show contestants, they must first have each contestant rank all members of the opposite sex in order of preference.
Then, on the first day at the villa, each woman proposes marriage to the man of her first choice. Some men receive many marriage proposals, while others receive no proposals at all. Each male then rejects all but the more preferred suitor, resulting in some participants becoming provisional matches, while others remain unpaired. .
On the second day, each rejected woman proposes to her second choice (even if the other is already paired). The men consider new proposals, but some may abandon their current match if a new suitor is better. And some newly heartbroken women even propose to their next potential partner.
This process is repeated as many times as necessary, starting on the third and fourth day, until everyone is in agreement. Although not everyone will be happy with pairing using this process, it is mathematically guaranteed that no one will want to be with each other more than the person they are currently with ( Assuming your preferences haven’t changed since we met, that is). Although this is not a guarantee, love island The spin-off is drama-free, relaxing viewing, and is probably as good as we get.
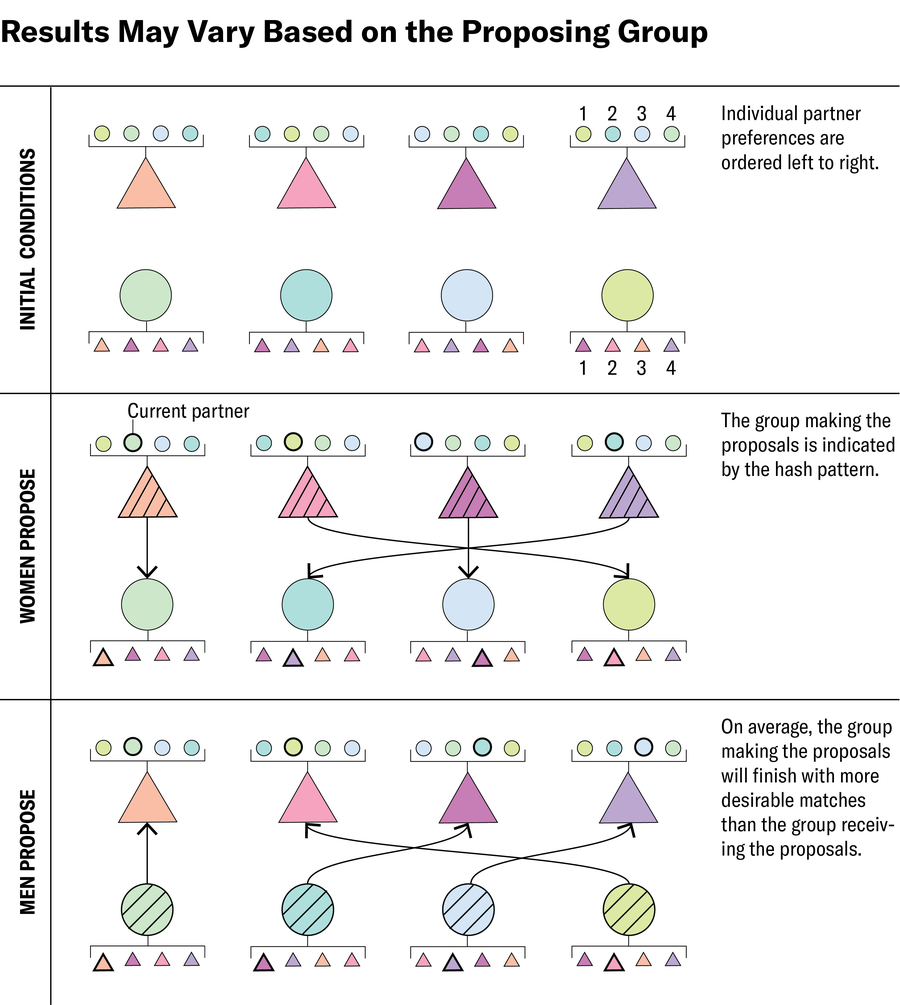
Interestingly, the group that proposes first has an advantage. When women propose first, they make a more desirable match, on average, than men. “The problem with Gail Shapley is that there are extreme games on both sides,” said Vijay Vazirani, a computer scientist at the University of California, Irvine.
The results may be a little lopsided, but you can’t beat Gale and Shapley’s strategy. And as it turns out, this version has already been used since the 1950s by an organization that matches medical students to training programs across the country. In 1984, Stanford University economist Alvin Ross used the mathematical language of Gale and Shapley to demonstrate that the process used by this organization not only ensures stable matching, but also “strategy-proofs,” that is, the system We have shown that there is no way to exploit it. This feature, more commonly referred to as incentive compatibility, is highly valued because it means that everyone can ultimately choose the best option if they honestly report their preferences.
Ross and economist Elliott Peranson also made some adjustments to the algorithm. They adapted it for medical students who are married and want to complete their training at the same location. They also pointed out that the benefit to residents would be short-lived because the hospital offered first. Ross recommended that residents make their proposals first to ensure they get the best outcome. To this day, hospitals and inpatients rank each other, mathematically calculated to ensure stable conditions are achieved. Ross and Shapley were awarded the Nobel Prize in Economics in 2012 for their work.
Ross and his colleagues also used this mathematical language to tackle another tricky matching problem: assigning children to public schools in America’s largest cities. In 2003, they adapted Gail Shapley to assign students to New York City’s notoriously competitive public high schools. In its first year of operation, the number of students matched to one of their first choices increased from approximately 50,000 to more than 70,000. Another version of the algorithm is also used to assign students to Boston public schools.
And back in the love realm, Gail Shapley’s algorithms are even influencing the inner workings of dating apps like Hinge. Although users do not explicitly rank potential matches, these apps look at a user’s history of likes and dislikes and their stated dating preferences to handpick a small number of “top matches.” , first displayed to the user. The likes and messages sent to potential matches are similar to the original algorithm’s suggestions.
“The power of models like[Gail Shapley’s]is that they abstract ideas across a variety of settings,” emphasizes John Kleinberg, a computer science professor at Cornell University. Problems that span different domains “may have conceptual similarities,” he says, and Gail Shapley’s algorithms “give us a mathematical language to talk about[them].” ” says.
Although this algorithm is simple and reliable, it can also exacerbate existing imbalances if the rankings are biased. Admissions data obtained by The City, a nonprofit news organization based in New York City, shows that in big city high schools, especially many top-performing schools, black and Latino students are far more likely to be white or Asian than white or Asian. showed that they were regularly selected for admission at a lower rate than other students. Residency match programs have been found to have similar shortcomings in terms of racial and gender equity.
“The real problem is not the algorithms themselves, but the ranking data they use and the environment in which they are deployed, explains Utuk Umbar, an economics professor at Boston University. We see it throughout the artificial intelligence boom”: Complex algorithms learn to reproduce patterns in data, and therefore often reproduce our biases as well.
“If humans are biased, that bias is in the data,” says Eva Tardos, a computer science professor at Cornell University. Researchers have suggested several ways to combat data bias. For example, institutions such as hospitals and schools can use larger, more diverse panels of judges to rank candidates. Additional algorithms can also be used to account for known biases by changing the ranking weights before they are used for matching.
Of course, there is no algorithm that can guarantee a happy marriage when it comes to marriage or education. But the best options remain the ones that are simple, transparent, and encourage honesty, so 60 years later, it seems hard to beat the Gail Shapley algorithm.