Pi (π) shows up in the most unlikely places. It can be found in pendulums, springs, and river bends, not to mention circles. This everyday number is connected with transcendental mystery. It has inspired Shakespearean mind puzzles, baking challenges, and even original songs. And pi continues to surprise. Most recently, in January 2024, physicists Arnab Priya Saha and Aninda Sinha of the Indian Institute of Science announced an entirely new formula for calculating pi, which they later published in November 2024. Physics Review Letter.
Saha and Sinha are not mathematicians, and they weren’t searching for a new equation for pi. Rather, the two string theorists were working on a unified theory of fundamental forces that could reconcile electromagnetism, gravity, and the strong and weak forces. In string theory, the fundamental building blocks of the universe are not particles like electrons or photons, but tiny threads that vibrate like guitar strings and give rise to all visible phenomena. In their work, Saha and Sinha investigated how these strings interacted, and stumbled upon new formulas related to important mathematical quantities.
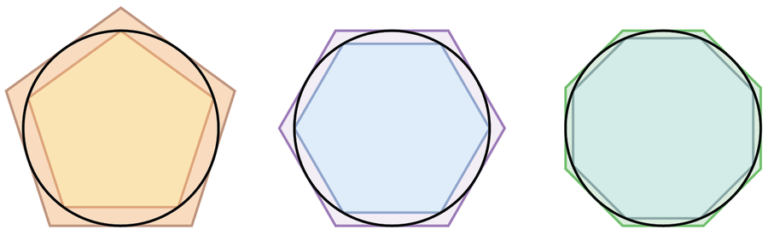
Humanity has been trying to determine the exact value of pi for thousands of years. This is not surprising, considering that it can be used to calculate the circumference and area of a circle. Even ancient scholars developed geometric approaches to calculate this value. One famous example is Archimedes, who estimated pi with the help of polygons. yeahBy placing a one-sided polygon inside a circle and a one-sided polygon outside it, and calculating the perimeter of each, we were able to narrow down the value of pi.
Supporting science journalism
If you enjoyed this article, please support our award-winning journalism. Subscribe. By purchasing a subscription, you help ensure a future of influential stories about the discoveries and ideas shaping the world today.

A common way to determine pi geometrically is to draw a bounding polygon on the inside and outside of the circle and compare the two perimeters.
Fredrik/Leszek Krupinski/Wikimedia Commons
In school, teachers often introduce this method. Even if you don’t remember it, you can imagine that the process is quite complicated. Archimedes proved that Pi is between 3.1408 and 3.1429 by comparing the perimeters of polygons with 96 vertices. Therefore, this method is not very practical for calculating Pi accurately.
Infinite series to determine Pi
In the 15th century, experts discovered an infinite series, a new way to represent pi: by adding the numbers together, one by one, you get the value of pi, and the more addends you use, the more accurate the result will be.
For example, the Indian scholar Madhava, who lived from 1350 to 1425, discovered that pi is equal to 4 multiplied by a sequence that starts with 1 and alternately subtracts or adds fractions placed on successively larger odd numbers (i.e., 1/3, 1/5One way to express this is:

This formula allows us to accurately calculate Pi in a very simple way. You don’t need to be a math whiz to solve this equation. However, do Be patient; it will take a long time to get an accurate result; even if you evaluate 100 addends, the result will still be off the mark.
As Saha and Sinha discovered over 600 years later, Madhava’s formula is just a special case of a more general equation for calculating Pi. In their work, string theorists discovered the following formula:
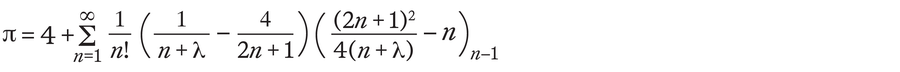
This formula produces an infinitely long sum. It is noteworthy that it depends on a coefficient λ, a freely selectable parameter. Whatever the value of λ, the result of the formula will always be pi. And because there are an infinite number of numbers that can correspond to λ, Saha and Sinha found an infinite number of formulas for pi.
When λ is infinitely large, the equation corresponds to Madhava’s formula: λ appears only in the denominators of fractions, so the corresponding fractions for λ = ∞ are zero (because fractions with large denominators are very small). Thus, when λ = ∞, Saha and Sinha’s equation has the form

The first part of the equation already resembles the Madhava formula. We add together fractions with odd denominators. The last part of the sum (–yeah)1stHowever, it is not very familiar. yeah – 1 is the so-called Pochhammer symbol. In general, the formula (One)yeah Corresponding to the product One x(One + 1) x (One + 2) x … x (One + yeah – 1) For example, (5)3 = 5 x 6 x 7 = 210. Then the Pochhammer symbol for the above equation becomes: (–yeah)yeah – 1 = (–yeah) x (–yeah + 1) x (–yeah + 2) x … x (–yeah + yeah – 3) x (–yeah + yeah – 2).
A few steps towards the Madhava formula
These factors may look complicated at first glance, but they can be easily simplified: First, subtract -1 from each factor, so the sign in front of the big product is -1. yeah is odd, and if +1, yeah Since it is an even number, (–yeah)yeah – 1 = (–1)yeah x yeah x (yeah – 1) x (yeah – 2) x … x (yeah – yeah + 3) x (yeah – yeah + 2) The last element can be simplified further: (–yeah)yeah – 1 = (–1)yeah x yeah x (yeah – 1) x (yeah – 2) x … x 3 x 2 x 1.
This long expression is actually (–yeah)no 1 = (–1)yeahx yeahThe result will be:

This corresponds to Madhava’s formula. Therefore, the equation discovered by Saha and Sinha also contains the sequence discovered by Madhava.
But as the two string theorists report, pi can be computed much faster for smaller values of lambda: Madhava’s result requires 100 terms to converge to within 0.01 of pi, while Saha and Sinha’s lambda = 3 formula requires only the first four summands. “While[Madhava’s]series takes 5 billion terms to converge to 10 decimal places, our new representation for lambda between 10[and]100 takes only 30 terms,” the authors write in the paper. But Saha and Sinha didn’t just figure out the most efficient way to calculate pi; other sequences have been known for decades that provide surprisingly accurate values much faster. In this case, what’s really surprising is that the physicists came up with a new formula for pi while writing a paper describing string interactions. They developed a way to show the probability that two closed strings will interact, something many string theorists have been searching for for decades without success.
Upon closer inspection of the resulting equations, Saha and Sinha realized they could express pi and the zeta function in this way. The zeta function is at the heart of the Riemann hypothesis, one of the greatest unsolved mysteries in mathematics. Given their interest to string theorists, the formulas for pi and the zeta function only appear in the paper’s final paragraphs. “Of course, our motivation was not to find an equation for pi,” Sinha said in a Numberphile YouTube video. “Pi was just a by-product.”
This article was originally published on The scientific spectrum Reprinted with permission.