Sometimes intuition can lead one astray: especially in mathematics, one constantly encounters results that seem impossible: infinity does not necessarily equal infinity, for example, or a turtle can overtake a human athlete, at least from a certain mathematical point of view.
There are many scenarios that seem at first (or second or third) contradictory. However, these paradoxes can be explained. They are not errors, but warnings against relying too much on intuition in mathematics. Here are three of the strangest paradoxes in the field.
Hilbert Hotel
Supporting science journalism
If you enjoyed this article, please support our award-winning journalism. Subscribe. By purchasing a subscription, you help ensure a future of influential stories about the discoveries and ideas shaping the world today.
Imagine you are traveling to a city and forgot to book a room in advance. By some stroke of luck, you come across a beautiful hotel named after the famous mathematician David Hilbert, whom you greatly admire. When you go to the reception, you discover that the hotel has an infinite number of rooms. The room numbers correspond to the natural numbers 1, 2, 3, 4, … and so there is no end to them.
However, the receptionist says that the hotel is fully booked. However, you are good at math and are not so easily fooled. You know a trick that will help you and all the other countless guests find a room: you suggest to the receptionist that each guest move to the room numbered one higher than their current room. That is, the person in room 1 should move to room 2, the person in room 2 should move to room 3, and so on.
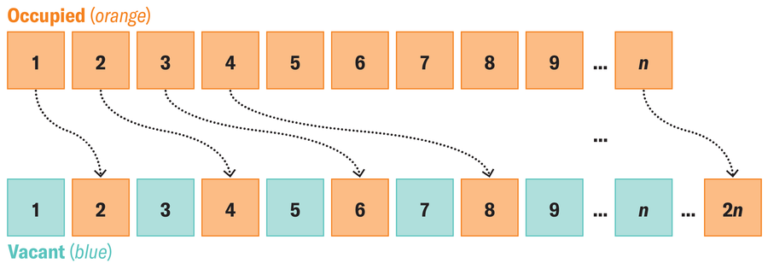
Hilbert’s hotel has no limit on the number of rooms that can be booked, so even if it is fully booked, there is still room for more guests. And not just one person; they could bring in a busload of passengers who want the same room. In this case, the hotel guests would have to move to multiple room numbers, not just one.
Even more strangely, if you bring an infinite number of people to Hilbert’s hotel, you could still fit them into a full hotel – the guest in room 1 would have to move to room 2, the guest in room 2 to room 4, the guest in room 3 to room 6, and so on. If each person moves to a room twice their current room number, there will be an infinite number of odd-numbered rooms free.
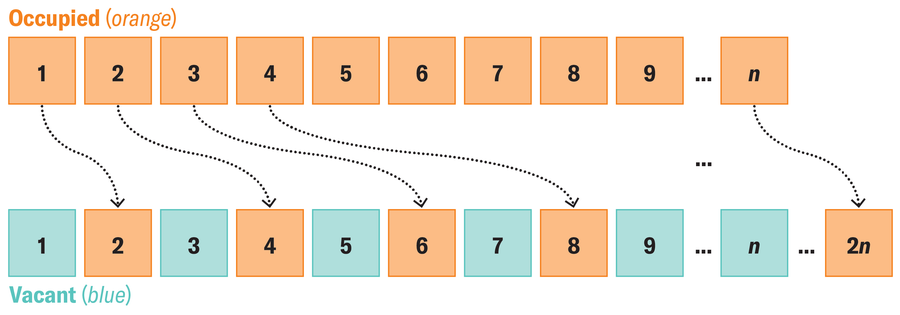
By moving each guest to a room with twice the number of their current room, space is made for an unlimited number of additional guests.
Jan Beránek/Wikimedia (CC BY-SA 4.0), styled by Amanda Montañez
German mathematician David Hilbert proposed this paradox in his lectures on infinity in 1925. This example shows that not all concepts can be transferred from the finite to the infinite. The statements “All rooms are full” and “The hotel cannot accept any more guests” are synonymous in the real world, but not in the infinite world.
The birthday paradox
The following paradox is well known to many. When I was a student, it was not uncommon for several of my classmates to have birthdays on the same day. In fact, I shared a birthday with one of my classmates. At first, this seems like a huge coincidence. After all, a year has 365 days (366 days in leap years, but we will ignore them for simplicity), and a school class consists of around 20-30 students. Therefore, our intuition tells us that it is unlikely that two children will be born on the same day.
But that’s not true. In fact, there is a greater than 50 percent chance that two people in a group of 23 people will have the same birthday. To understand this better, it helps to look at the number of pairs, rather than the number of people. With 23 people, there are (23 x 22) / 2 = 253 possible pairs, which is more than half of all the days in a year. However, if you look at the probability that one of the students in a class of 23 is born on a particular day, the chance is only 1- ((365-1) /365)^23=6.1 percent.
Thus, the birthday paradox arises from the fact that looking at pairs of students gives us more possibilities than looking at just individuals.
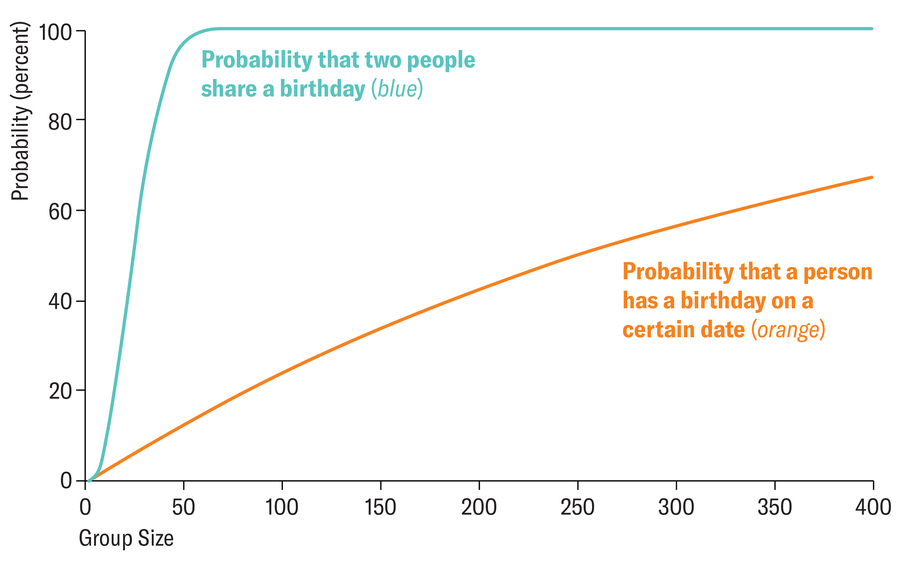
The blue line represents the number of people in a group (group sizes are listed in the table) x Two people on the axis have the same birthday. The orange line corresponds to the probability that a person has a birthday on a particular day.
Toobaz/Wikimedia (CC BY-SA 4.0), styled by Amanda Montañez
This fact has concrete effects, for example, in cryptography. When signing a digital contract, a “hash function” is used: the document is converted into a fixed-length string (the “hash”) when signed. Any change to the original document will result in a completely different hash being generated from it. By keeping the hash, the signer can prove what they originally signed, making it tamper-proof. However, the chances of two completely different documents generating the exact same hash are extremely slim, which poses a security risk.
As a rule, the length of the hash function is chosen so that such “collisions” (two different data records producing the same hash) are extremely rare. However, a hacker can perform a “birthday attack” – generate different documents and compare their hash functions pairwise, similar to a teacher comparing the birthdays of classmates, rather than focusing on a specific date and one student.
In practice, a birthday attack works like this: First, you create two contracts, V1 and V2. V1 is a fair contract, but V2 has some wording that favors you. Then, you modify both contracts in various places. You create variations of V1 and V2 by adding spaces, tabs, and newlines. These modifications are mostly invisible to a reader, but they drastically change the hash function of the document.
A pairwise comparison of the individual hash functions of modified contracts V1 and V2 can find a matching hash much faster than if you were to specifically try to reproduce a particular hash (say the hash of V1). If you find a matching pair of V′1 and V′2, you can have someone sign contract V′1 and later claim to have signed V′2. Because they both produce the same hash, your digital signature software cannot detect any fraud.
Russell’s Antinomy
British philosopher Bertrand Russell invented the paradox, also known as Russell’s antinomy, in 1901. An antinomy is a statement that states two seemingly contradictory ideas. Unlike Hilbert’s hotel and birthday paradoxes, Russell’s antinomy is not simply a result that evades our intuition; it violates the very rules of logic. An antinomy produces a statement that is neither false nor true.
There are several examples that illustrate Russell’s antinomy, but one of the most famous is the “barber’s paradox.” Suppose a barber shaves every unshaven man in a town. Then, only Does the barber shave himself? If he does, then he is no longer in the group of people who do not shave themselves. But if he does not shave himself, then by definition he must shave himself (since all the residents who do not shave themselves go to him).
The problem arises because of an insufficient definition of a set. At the time Russell published his antinomy, a set generally referred to a collection of things. For example, the natural numbers form a set. So does the collection of all inhabitants who do not shave. This allows a set to also subsume itself or refer to itself as a whole, but these properties lead to a contradiction. This antinomy therefore led to the demise of what mathematicians call “naive set theory”.
The foundations of mathematics continue to rely on set theory, but the sets in this construction are not just sets, but must satisfy certain conditions: for example, a set must be constructed from existing sets, and cannot refer to itself, which eliminates contradictions such as the Barber’s Paradox.
Expressed mathematically, this means that all men in a town who are allowed to grow beards form a set. MaThe set includes men who shave and men who don’t. C This includes all barbershop customers. CWe must follow the rules of modern set theory: if a barber finds a man with a beard, or MaThe customer set is “all “A male resident who does not shave” – in this case the definition would refer to both the barber and the customer as part of it. MaSet theory does not allow such a definition. But if barber is not part of the set, then MaFor example, if the barber was a woman or could not grow a beard, the definition would be permitted.
Now we can breathe easy: the paradox has been resolved and mathematics is not doomed to fail. But there is no guarantee that the rules of mathematics will not one day produce an unresolvable contradiction. Logician Kurt Gödel proved this in the 1930s, making clear that there is no guarantee that mathematics will work in a self-contained way forever. The best we can do is hope that an unresolvable contradiction never arises.
This article was originally published on The scientific spectrum Reprinted with permission.